Contents

False positive vs false negative tradeoff¶

In binary classification problems, there are two types of errors that can happen:

  1. False positive (False alarm) we estimate \(\hat{y} =1\) but the truth is \(y =0\)

  2. False negative (Missed detection) we estimate \(\hat{y} = 0\) but the truth is \(y =1\)

We can define a define a different loss to different scenarios:

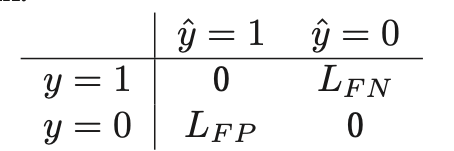
Where:

  • \(L_{FP}\) is the cost of false positive

  • \(L_{FN}\) is the cost of false negative

Given these 2 values we can define a threshold how to classify if:

\(L_{FN} = cL_{FP}\) , than we should pic \(\hat{y} = 1\) iff \(\frac{p(y = 1|x)}{p(y=0|x)} > \tau, \tau = \frac{c}{1+c}\) . For an example if the cost of false negative is twice as much as false positive, \(c=2\) than we use a decision threshold of 2/3.

ROC curves¶

ROC cures to generalize this FP-FN tradeoff.

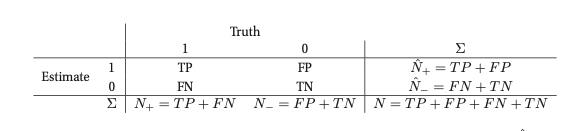
Rock Table

  • \(N_+\) is the true number of positives

  • \(\hat{N}_+\)is the estimated number of positives

  • \(N_-\) is the true number of negatives

  • \(\hat{N}_-\) is the estimated number of negatives

Confusion matrix¶

Confusion matrix

  1. True positive rate (TPR) (Sensitivity, recall or hit rate)

    \[TPR = TP/N_+ \approx p(\hat{y} =1|y=1)\]

  2. False positive rate (FPR) (False alarm rate, type 1 error)

    \[FPR = FP /N_- \approx p(\hat{y} = 1|y=0)\]

  3. False negative rate (FNR) (Miss rate, type 2 error)

    \[FNR = FN/N_+ \approx p(\hat{y}=0|y=1)\]

  4. True negative rate TNR (specifity)

    \[TNR = TN /N_- \approx p(\hat{y}=0|y=0)\]

Now we can plot the ROC which is just ration between TPR and FPR for a waring threshold \(\tau\)

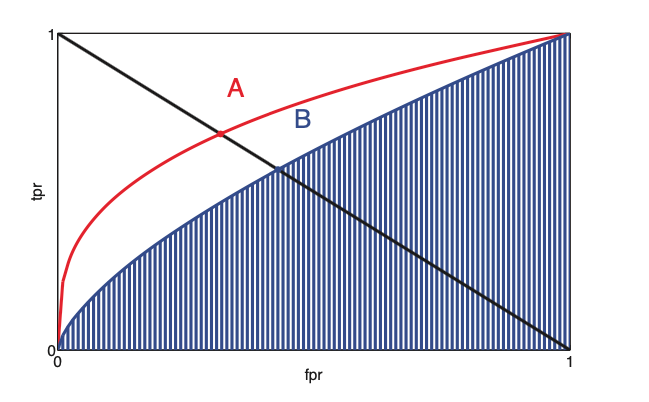(A is better than B)

We can characterize this curve as single number summary, if we take the area under the curve. (ROC AUC). Where the higher AUC the better the performance.

Precision recall curves¶

In cases that we have very little positive samples, or in cases where the notion of negative is not well defined we can use precision recall curve instead.

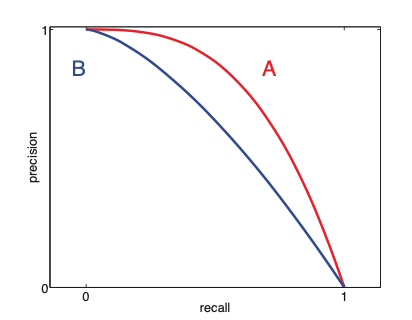
(A is better than B)

Precision¶

\[TP/\hat{N}_+ = p(y=1| \hat{y}=1) = \frac{\sum_i y_i \hat{y}_i}{\sum_i \hat{y}_i}\]

Recall¶

\[TP/N+ = p(\hat{y} = 1| y =1) = \frac{\sum_i y_i \hat{y}_i}{\sum_i y_i} \]

F-Scores¶

For a fixed threshold we can compute a single precision and recall value, and combine them in a single statistics the F-score, or F1 socre which is the harmonic mean of precision and recall:

\[F1 \triangleq \frac{2PR} { R + P}\]
Boostrap Cross correlation