Classical PCA¶
Suppose we want to find an orthogonal set of L linear basis vector \(w_j \in R^D\) and the corresponding scores \(z_i \in R^L\), such that we minimize the average reconstructuion error
\(\hat{x}_i = Wz_i\)
\(W\) is contrant to be orthonormal
\(Z_{N \times L}\) matrix with \(z_i\)
\(||A||_F= \sqrt{\sum^m_i \sum^n_j a_{ij}^2} = \sqrt{tr(A^TA)}\) is the forbenius norm of a matrix A
The optimal solution is obtained by setting \(\hat{W} = V_L\) where \(V_L\) contains the L eigenvectors with largest eigen values of the empirical covariane matrix \(\hat{\Sigma} = \frac{1}{N} \sum_i^N x_i x_i^T\) where we assume that \(x_i\) has zero mean. The optimal low-dimensional encoding of the data is given by \(\hat{z}_i\) which is an orthogonal projection of the data on the column spaned by the eigen vectors.
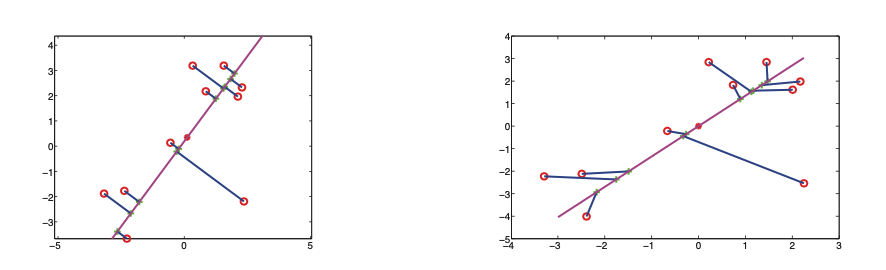
Example of PCA and probabilistic PCA. We can see that the data points are orthogonaly projected on the line. The second picture is probabilistic PCA here the projection is no longer othogonal.
Maximizing the variance¶
There is an alternative view to the minimization of reconstruction error is to view this process as variance maximization.


