Belief propagation¶
If we want to use variable elimination compute the marginal for \(p(x_i)\), we can find an optimal ordering by rooting the tree at \(p(x_i)\) and iterating trough nodes in post-order.
This is optimal, the largest clique formed during VE has size 2. At each step we compute the factor \(\tau_k\) which eliminates \(x_j\):
\(x_k\) is the parent of \(x_j\) in the tree.
\(\tau_j(x_j)\) can we viewed as a message that \(x_j\) sends to \(x_k\) that summarizes all the information from subtree rooted at \(x_j\)
At the next step we pass \(\tau_k(x_k)\) to \(x_l\) (parent of node \(x_k\)) to be marginalized out:
There \(\tau_k\) sends all the information about the subtree rooted at \(x_k\) up its parent \(x_j\). This process goes on until we reach the root node \(x_i\), here we receive information from all of its intermediate children, marginalizing them out to get the final marginal.
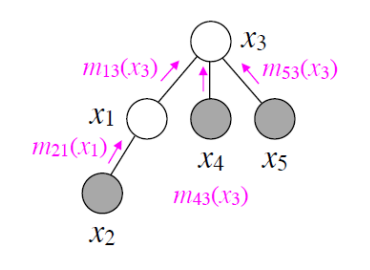
This message passing can be visualized using arrows on a tree:
We use VE to compute the marginal of \(x_3\)
Now if we want to compute the marginal for \(p(x_k)\) we run VE with \(x_k\) at the root, waiting until \(x_k\) receives all messages from its children. The key is that \(x_k\) receives from \(x_j\) is the same as it received when \(x_i\) was at the root, because of this we can quickly compute the marginal. The only messages we need to recompute are those from \(x_i\) to \(x_k\).
This message passing algorithm can be summarized as follows:
A node \(x_i\) sends a message to a neighbor \(x_j\) whenever it has received messages from all nodes besides \(x_j\). This happens after precisely \(2|E|\) steps, since each edge can receive messages only twice once form \(x_i \rightarrow x_j\), and once from the opposite direction.
Variants¶
Sum product message passing¶
Used for marginal inference (computing \(p(x_i)\)) it is the generalization of forwards-backwards) algorithm from chains to trees.
Max-product message passing¶
Used For MAP inference (computing \(\max_{x_1, \cdots, x_n} p(x_1, \cdots, x_n\))