One dimensional motion¶

We move along an single axis, from $x_1$ to $x_2$.

Displacement¶

Is a vector valued quantity where we move from one point to the other. It is defined by a starting postion ending position and a direction in which an object moves.

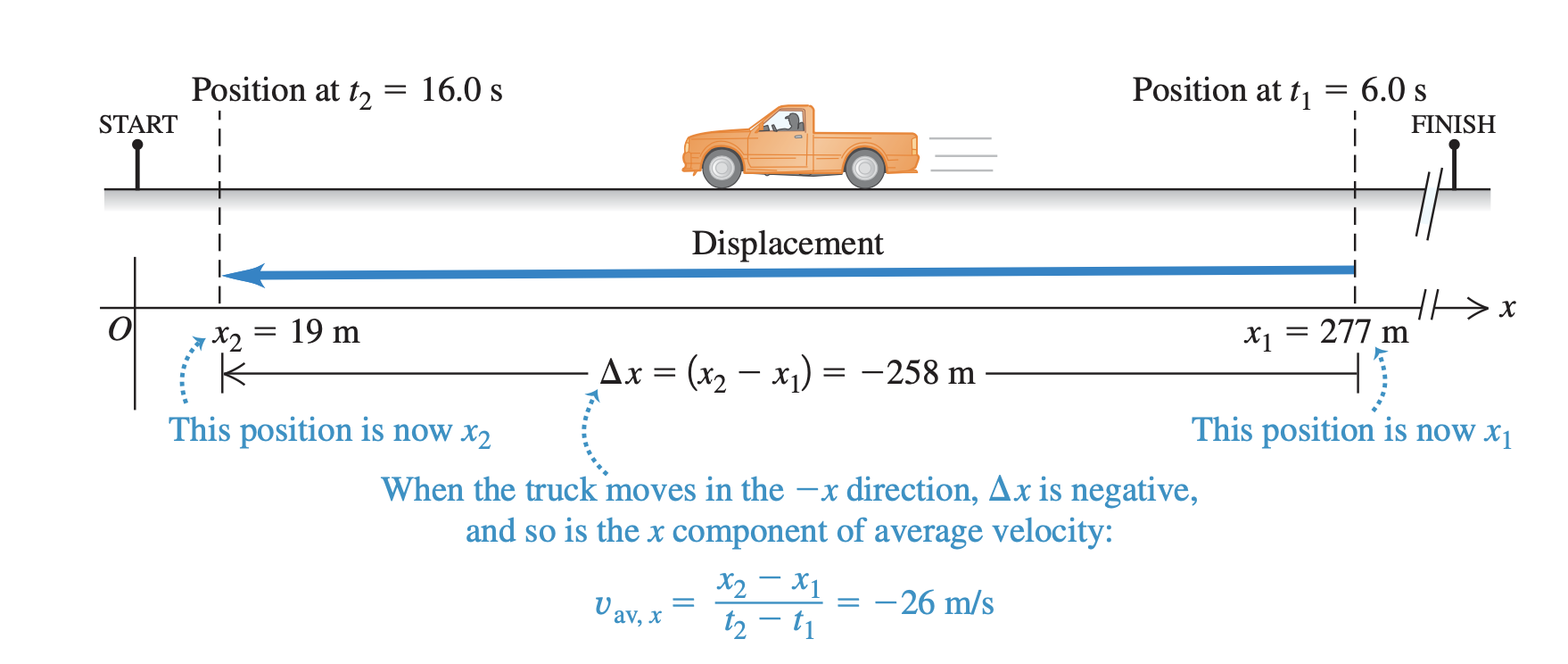
The initial position $x_1 = 277m$ to the ending position $x_2=19m$ thus the displacement $\Delta x = -258m$

Since the value is negative, we know in which direction an particle is moving. (we have only one dimension)

Velocity¶

Is a vector valued quanity, since we allways divide the displacement by time.

Average velocity¶

\[ v_{av} = \frac{\Delta x}{\Delta t} \]

$\Delta x = x_2 - x_1$
$\Delta t = t_2 - t_1$

It is the displacement divided by the time it took to displace.

Example: An car is at $t_1 = 1s$ in position $x_1 = 19m$ and moves along the x axis. At $t_2=4s$ is at $277m$ The average veloity is $$v_{av} = \frac{277-19}{4-1} = 86 \text{m/s}$$

We can express the movement of a particle along a straight line as function:

\[ x = f(t) \]

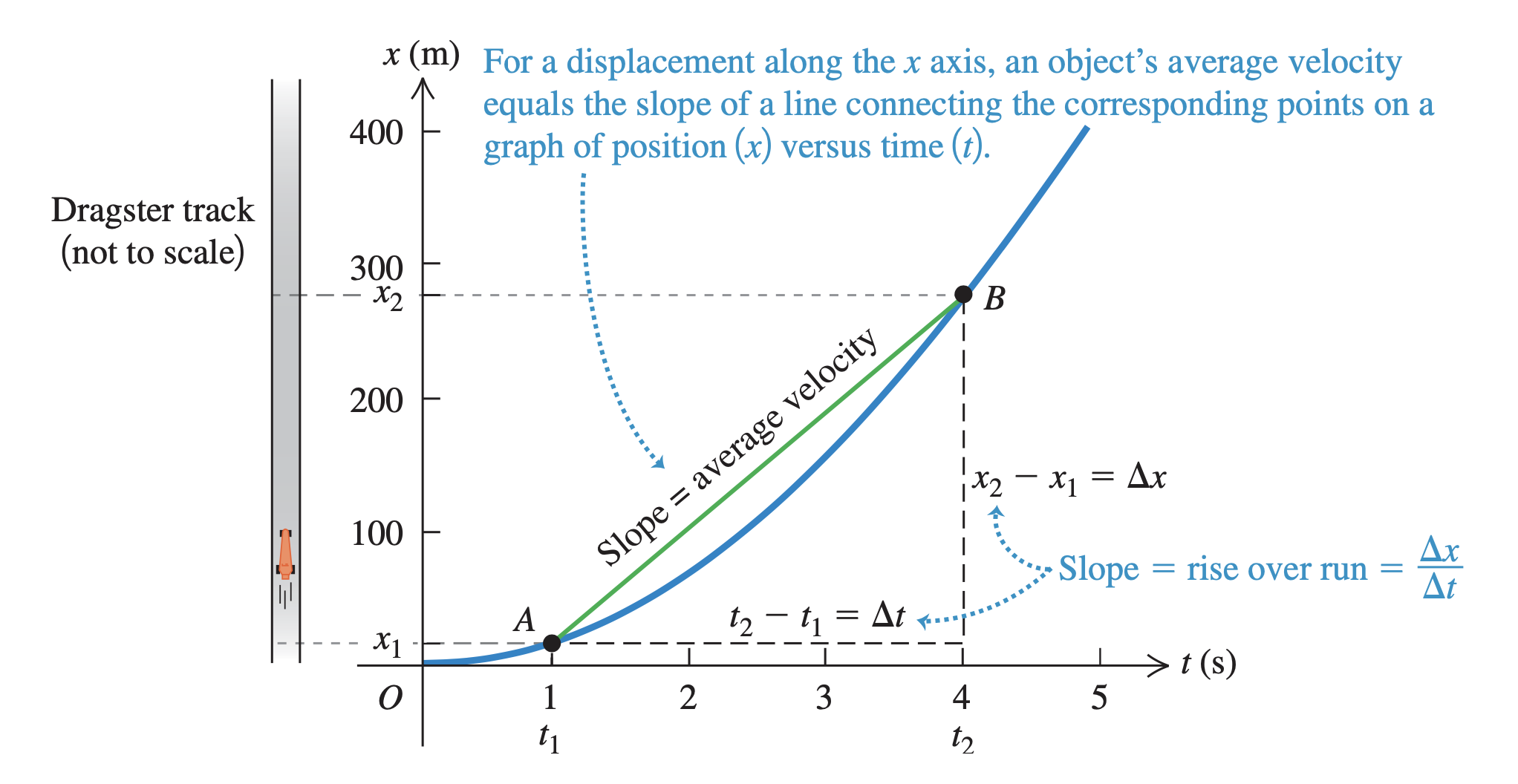
The average velocity between two positions is the slope of a line connecting the two corresponding points on a graph of position as a function of time.

Instantaneous velocity¶

In general velocity is not constant, the instantaneous velocity is the velocity of a particle at any one specific instant of time or point in path.

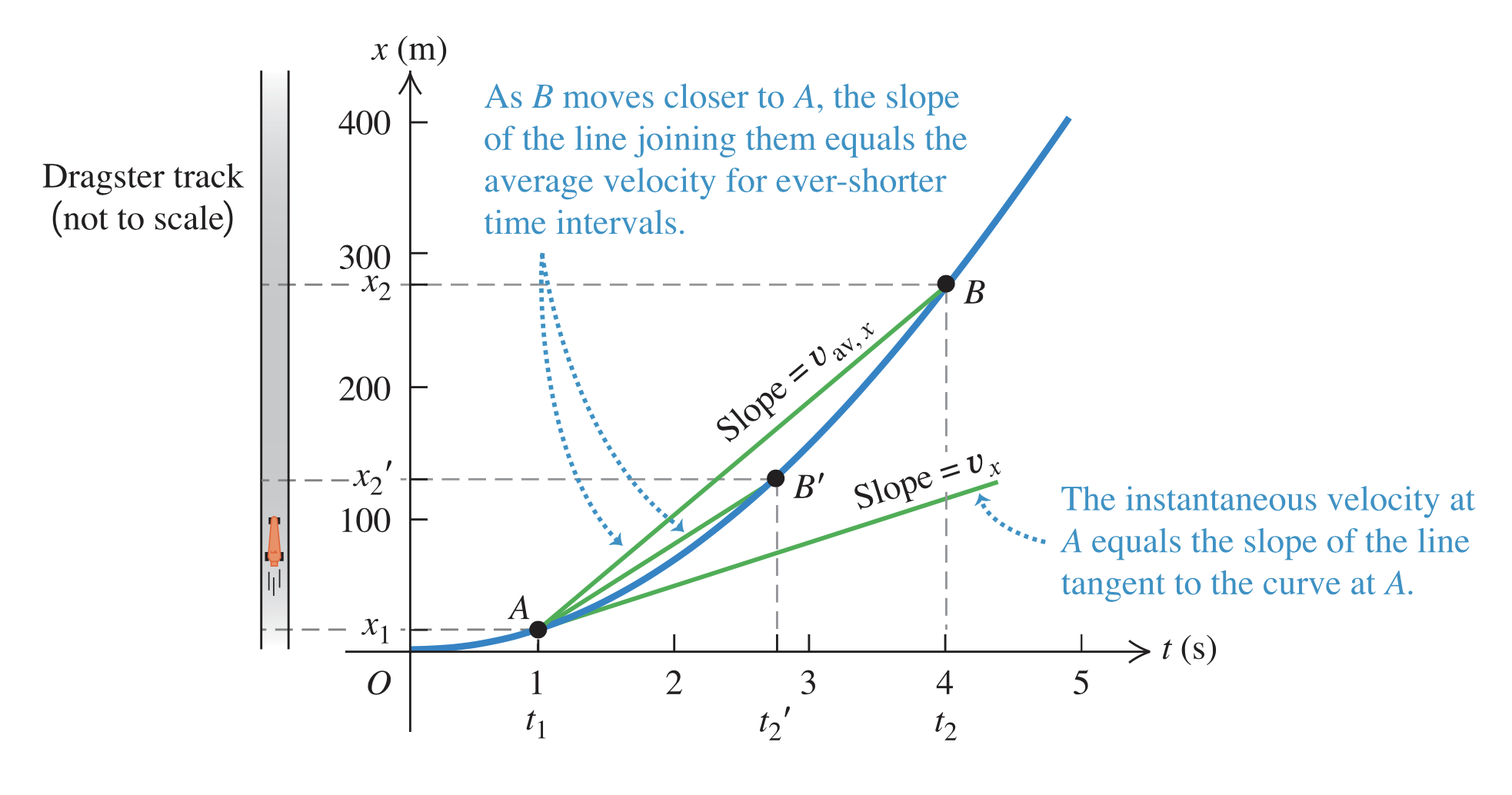
\[ v_x = \lim_{\Delta_t \rightarrow 0} \frac{\Delta x}{\Delta t} \]

The instantaneous velocity at any point is equal to the slope of the tangent line to the curve at that point.

Acceleration ¶

Here we accelerate in one dimension, mostly focusin on constant acceleration.

study-notes