Contents

Exponential distribution¶

Describes the waiting time for the occurrence of a single event given an constant rate.

\[ X \sim Expon(\lambda) \]

PDF¶

\[f(x|\lambda) = \lambda e^{-\lambda x} \]

  • \(\lambda\) rate at which events is expected to occur. The larger the rate the steeper the curve

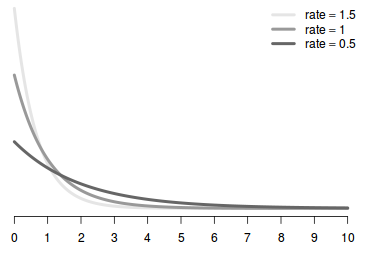
exponentail_distribution

Properties¶

  • is bounded \((0, \infty)\)

  • the mean and variance are booth related to the rate

    • variance = \(\frac{1}{\lambda^2}\)

    • mean = \(\frac{1}{\lambda}\)

Memory less property¶

This property only applies to the exponential distribution. It state that we wait an predetermined time for a success, it wont make that success more likely to occure.

Example: We want to know what is the probability that the event will occur if we wait for time \(t\) given that we already waited \(s\).

\[P(X \ge s + t | X \ge s) = \frac{P(X \ge s + t)}{P(X \ge s)} = \frac{e^{-\lambda(s+t)}}{e^{-\lambda s}} = e^{-\lambda t} = P(X \ge t)\]

Expectation From the view of the expectation:

\[E[X| X \ge s] = s + E[X] = s + \frac{1}{\lambda}\]

Connection to Gamma¶

The exponential distribution can be viewed as a speciial version of gamma distribution

\[Expon(x| \lambda) = Ga(x| 1, \lambda) \]

Poisson process¶

Exponential distribution describes the vaiting time of a single event in a poisson process

Gamma distribution Back-propagation through time